The Fibonacci series, named after the Italian mathematician Leonardo Fibonacci, is an infinite sequence of numbers that has captivated mathematicians, biologists, artists, and philosophers for centuries. It appears mysteriously in a wide variety of scientific and natural contexts and has become an emblem of the unexpected mathematical beauty found in nature.
Understanding the Fibonacci Series
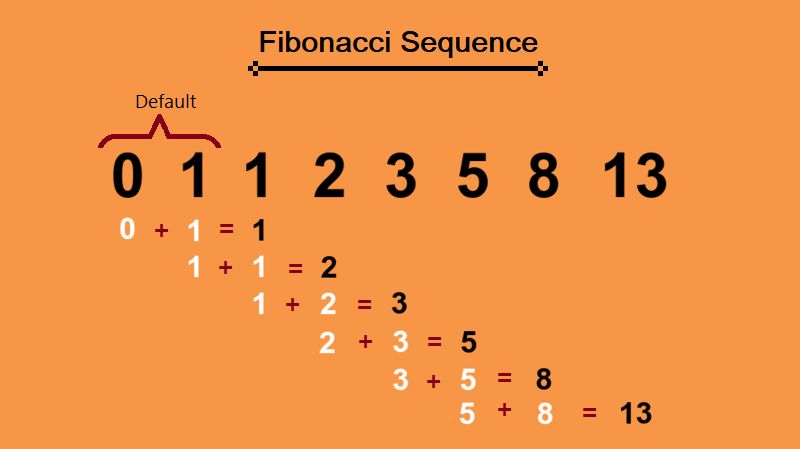
At its simplest, the Fibonacci sequence is a series of numbers where every number after the first two is the sum of the two preceding ones. Often starting at 0 and 1, the series goes: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so forth.
Written mathematically, the sequence is defined by the following recurrence relation:
1 2 3 | F(0) = 0, F(1) = 1, F(n) = F(n-1) + F(n-2) for n > 1 |
The Fibonacci sequence’s recursive nature means that any term in the sequence is directly related to the two terms before it. This property makes it an essential tool in various mathematical and computational problems.
Fibonacci Series in Nature and Science
In addition to its pure mathematical interest, the Fibonacci sequence has fascinating applications in the natural and biological sciences. It appears in numerous aspects of the natural world:
- Phyllotaxis: Many plants exhibit the Fibonacci sequence in the arrangement of leaves along the stem, which optimizes exposure to sunlight and rain.
- Reproduction of rabbits: This was actually the problem that introduced Fibonacci sequence. Fibonacci posed and solved a problem in the “Book of Calculation” involving the growth of a population of rabbits based on idealized assumptions.
- Pinecones and pineapples: The spirals on pinecones and pineapples reflect Fibonacci numbers.
- DNA: The Fibonacci sequence also appears in the structure of DNA, with one complete turn of the double helix measuring 34 angstroms in length and 21 angstroms in width (both Fibonacci numbers).
These are just a few of the many examples of where the Fibonacci sequence appears in the natural world.
Fibonacci Series in Computer Science and Algorithm
The Fibonacci series also plays a significant role in computer science. Algorithms to compute Fibonacci numbers are used to teach the fundamentals of programming, recursion, dynamic programming, and algorithmic efficiency.
Here’s a simple Python program to generate the Fibonacci series up to n:
1 2 3 4 5 6 7 8 | def fibonacci(n): fib_sequence = [0, 1] while len(fib_sequence) < n: fib_sequence.append(fib_sequence[-1] + fib_sequence[-2]) return fib_sequence # Print the first 10 numbers in the Fibonacci series print(fibonacci(10)) |
This code starts with a list containing the first two Fibonacci numbers, 0 and 1. It then enters a loop, which continues until the length of the list is the number of terms requested. On each iteration of the loop, it calculates the next Fibonacci number by adding the two most recent numbers in the list, and then adds this number to the end of the list.
When you run this code with the argument 10, it will print: [0, 1, 1, 2, 3, 5, 8, 13, 21, 34], which are the first 10 numbers in the Fibonacci sequence.
Conclusion
The Fibonacci series is a simple sequence of numbers with unexpected complexity and utility. Its interplay between number theory, nature, and computation provides a remarkable testament to the interconnectedness of mathematical concepts. Whether you’re counting petals on a flower, optimizing a computer algorithm, or simply enjoying the mathematical beauty, the Fibonacci sequence continues to captivate minds in many fascinating ways.
