Named after the ancient Greek mathematician Pythagoras, Pythagoras’ theorem is a fundamental principle in Euclidean geometry. The theorem plays a pivotal role in several branches of mathematics and physics, forming the bedrock for distance calculations, vector algebra, and trigonometry, among others.
Pythagoras’ Theorem: The Formula
Pythagoras’ theorem applies to right-angled triangles — triangles that include an angle of 90 degrees (π/2 radians). The theorem asserts that for any triangle with a right angle, the square of the hypotenuse’s length (the side opposite the right angle) is identical to the sum of the squares of the lengths of the remaining two sides. This can be written as:
1 | a² + b² = c² |
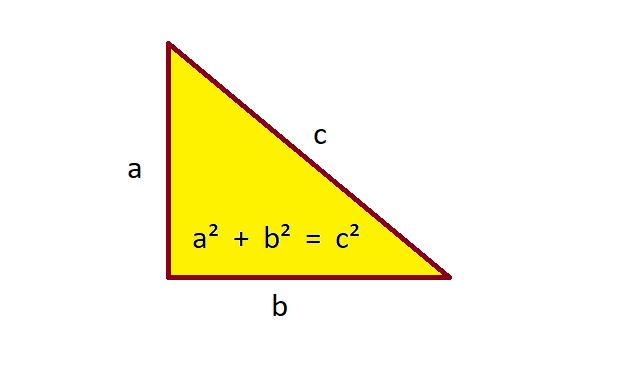
Where:
- `c` represents the length of the hypotenuse,
- `a` and `b` represent the lengths of the other two sides.
Pythagoras’ Theorem: The Proof
While Pythagoras’ theorem is attributed to Pythagoras, it was known and used by earlier cultures such as the Babylonians. However, the first recorded proof came from the ancient Greeks. Here, we will provide one of the simplest proofs, which doesn’t require any knowledge beyond basic algebra and geometry:
- Consider a square with side length (a + b) and draw four right-angled triangles inside this square, each with sides a, b, and hypotenuse c.
- The area of the square can be calculated in two ways:
- First, by its definition, which is side length squared, so the area is (a + b)².
- Second, by summing up the areas of the four triangles and the smaller square in the center. The area of each triangle is 1/2 * base * height = 1/2 * a * b, and since there are four such triangles, their total area is 4 * (1/2 * a * b) = 2ab. The area of the smaller square (whose sides are each of length c) is c².
- Setting these two expressions for the area of the large square equal to each other gives us:123(a + b)² = 2ab + c²a² + 2ab + b² = 2ab + c²a² + b² = c²
And there we have the Pythagorean theorem.
Pythagoras’ Theorem: Examples
Let’s put the Pythagorean theorem to use through a couple of examples:
- If one side of a right-angled triangle measures 5 units, the other side measures 12 units, what is the length of the hypotenuse?
By Pythagoras’ theorem, the length of the hypotenuse is the square root of the sum of the squares of the other two sides:
12345c = √(a² + b²)c = √(5² + 12²)c = √(25 + 144)c = √169c = 13 units - Suppose you know the lengths of the hypotenuse (10 units) and one side (8 units) of a right-angled triangle, what is the length of the other side?
By rearranging Pythagoras’ theorem, we get the length of the unknown side b is the square root of the square of the hypotenuse minus the square of the known side:
12345b = √(c² - a²)b = √(10² - 8²)b = √(100 - 64)b = √36b = 6 units
Conclusion
In conclusion, Pythagoras’ theorem is a fundamental principle in mathematics with a wide range of applications, including trigonometry, physics, computer science, and engineering. Understanding it well provides a solid foundation for further study in these fields.

