Though Windows is the well-known operating system among the common masses, the majority of developers and tech specialists prefer Linux…
Now that we’re halfway through the year, it’s the perfect moment to explore the standout Linux distributions of 2024. Linux,…
Git tags are like bookmarks for specific points in your project’s history. Imagine you’re reading a book and you use…
MySQL is one of the most popular open-source relational database management systems. It is still very common database among the…
Dig stands for Domain Information Groper and is a tool used to look up information in Domain Name Systems through…
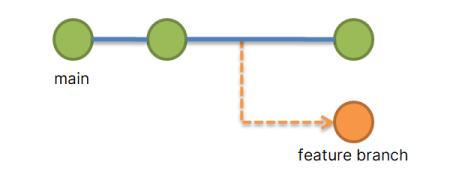
Imagine you and a friend are working together to build a website for a bakery. You want to keep the…
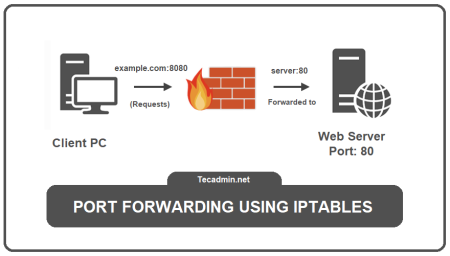
In real-life terms, Port forwarding is like telling the delivery driver where to go in a large apartment complex. Normally,…
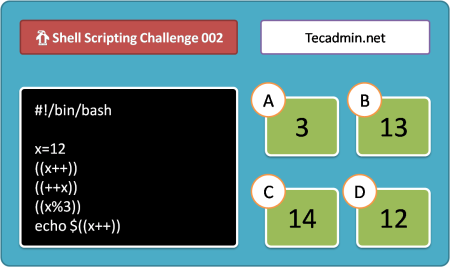
Welcome to Shell Scripting Challenge 002! In this challenge, we have created a simple Bash script with pre-increment, post-increment and…
Hey, Linux fans! Guess what? The team working on Ubuntu 24.10 have given it a special name: “Oracular Oriole”. Sounds…
Are you dealing with low RAM on your Ubuntu system? This is a common issue on systems required more memory…
As of writing this article, Node.js 20 is the latest LTS release, which is best suited for production servers. Alternatively,…
Welcome to our guide on installing Google Chrome, one of the most popular web browsers available today. This article will…